The PZ correction assumes
power balance based on the K and crack remain sharp. In addition, the condition of constant volume required by plastic
deformation 
has been
in this correction ignored. Neither of this presupposition is correct within of the EPFM, i.e. for ductile materials.
In fact, there is no theoretical basis for this correction and its application significantly distorts the real
relationship and because of this cannot be recommended.
As well known, ductile materials are able (due to plasticity) to reduce the crack (or notch) effect (stress redistribution, blunting). It has been shown, for years from Neuber with the stress concentration formula for the elipse of length 2a and end radius of curvature r subjected to an in-plane tension
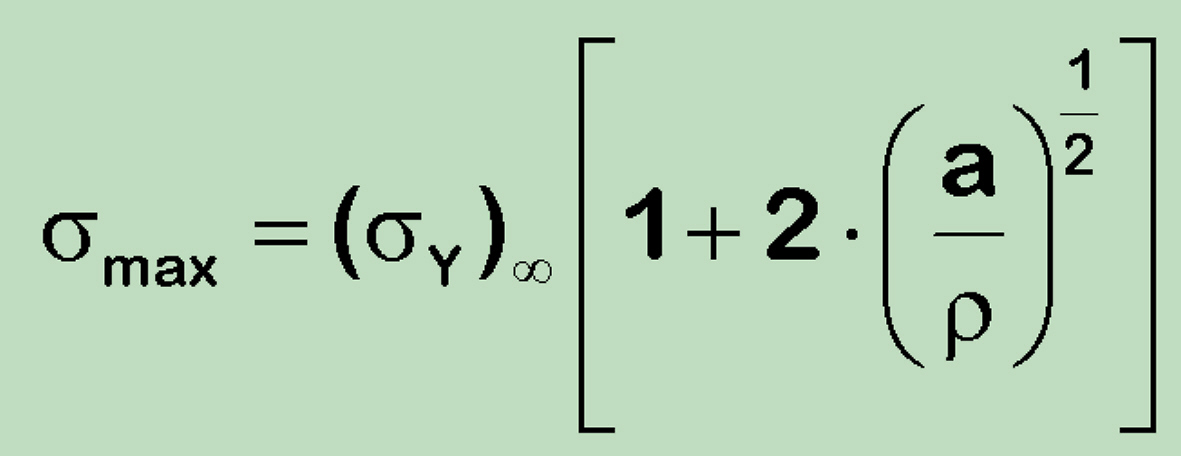
that the value of
is very sensitive to the size
of the crack tip root radius. As the root radius decreases below some minimum value, however, the magnitude of
may remain constant.
Independently, in case of ductile materials in the theory usually assumed sharp crack is in reality replaced with
a notch blunted under load, which is the physically more meaningful crack-tip representation for the investigation
of failure behaviour. To eliminate the effect of root radius, test specimens are usually used having the initial
machined crack extended by fatigue. This may not be necessary for very brittle materials.
On top of it, under the plane strain conditions, the correction is significantly smaller than under plane stress conditions, even though the corresponding situation becomes more severe. Therefore, if we consider that the PZ (plastic zone) at the crack tip represents, under the given conditions, the ability of the ductile material to reduce the stress peaks and thus to weaken the crack effect, the correction with the amount on the opposite side cannot be adequate.
As well known the Irwin's plasticity correction goes exactly in another direction (increase of crack size giving more severe stress intensity values).
A. Starting from the typical PZC relationship
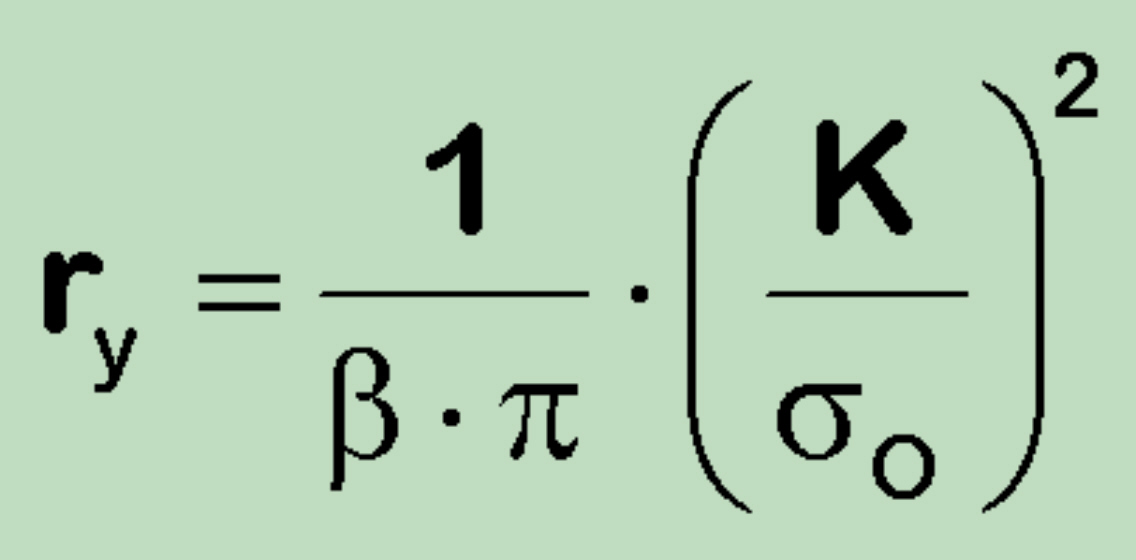
it can be shown that the
values of rp strongly depend on the selection of the 
, which should correspond to the mean stress within of the plastic
zone radius. A typical selection of engineering yield strength (with the 0.2% offset) is arbitrary. Considering the
singularity of the K-solution the corresponding stress level must be higher. We can assume flow or rupture strength
or even consider true properties.
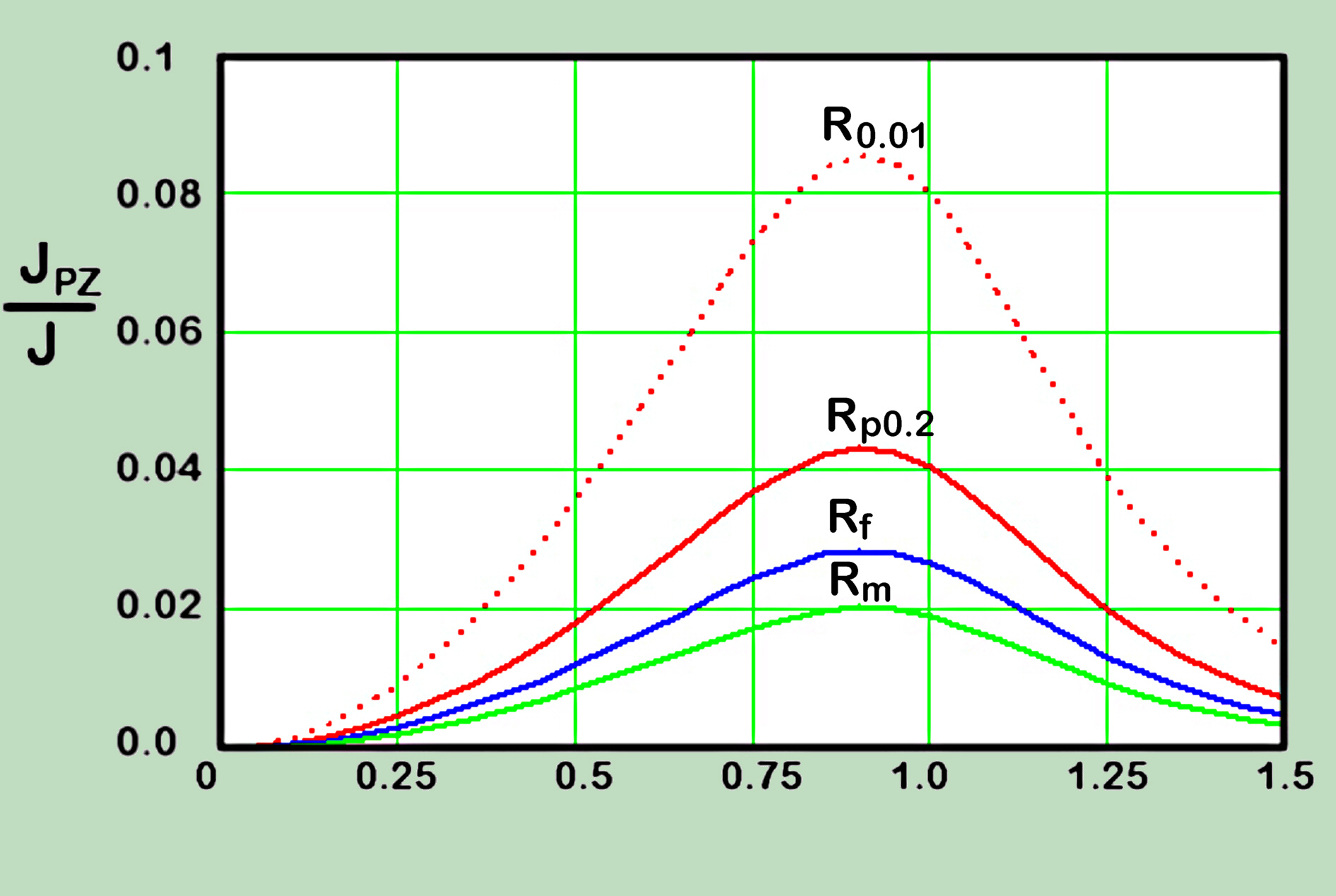
On the other side reducing the selection to the beginning of plasticity (0.01%) the values can be doubled.
B. The portion of the J-integral based on plastic zone correction may be evaluated according to the relationship
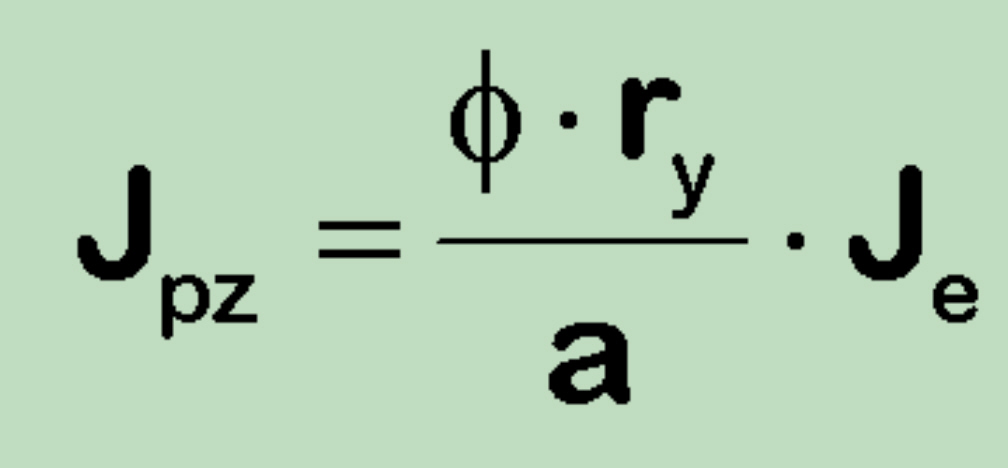
This shows that the corresponding J-increase is related to the a-increase and not to the strain increases (due to plasticity). This portion is also not affected by the biaxility even though the plastic term Jp is strongly affected.
C. For the same stress intensity values K, as long as the plastic zone is uniquely related to K only, in case of a small crack the plastic zone to crack size ratio is relatively larger and the applied stress higher than for a long crack. This means, for very small cracks the same K requires applied stresses more close to yield and the plastic zone becomes undefined. In addition, for short cracks the effect of local crack front irregularities and consequent local K and constraint variations are not averaged out. This brings out the effects of microstructural variations, which may even lead to different growth mechanisms.
D. As the K calculation is not based on stress balance for the reference section, then the PZ correction also cannot be based on balance. As the plasticity at the crack tip causes the increased opening of the crack this cannot be without effect to the stresses in the rest of the section.
E. The effective or adjusted crack length is sometimes determined experimentally using the compliance method especially in experiments intended to obtain the crack resistance curve. This method requires complex instrumentation and it is still not very clear how reliable is its application in calculating the loading curves K or J vs. a in an actual structure with entirely different loading and geometry.
Therefore, it becomes apparent that further progress in the field of fracture mechanics demands appropriate elastic-plastic solutions that can describe what occurs in the plastic zone as a function of loads and mechanical properties.
As a consequence, the plastic zone correction should be neglected in FAD construction until additional analysis establishes its general need and removes its arbitrariness.
It is clear that the plastic zone correction can be, if found necessary (for example for less ductile and less known materials) considered in the evaluation of Lr and Kr coordinates in FAD for a given case. For this, the PZC can be more exactly calculated using the relationships which are more better adapted to the actual situation. This will in any case produce more insighte and more accurate diagram relationships for the given situation.