Bei der einfachen Analyse der Schraubenverbindung wird von einer Verbindung mit einer Schraube ausgegangen, die durch eine Kraft, die irgendwo in der Schraubenachse angebracht ist, beansprucht wird. Obwohl diese eine sehr nützliche Vereinfachung ist, weil ein lineares Verhalten ergibt und zu einer einfacheren Berechnung führt, wirken die tatsächlichen Belastungen aber sehr selten, oder gar nicht, auf diese Weise.
Darüber hinaus ist die Verbindung mit nur eine Schraube selten. Bekanntlich sind die Vielschraubenverbindungen die grundlegende Form der Verbindung. Durch nicht linearen Verhalten, das von vielen Einflussgrößen abhängig ist, was in der Regel zu der massiven Erhöhung der Beanspruchungen in der Verbindung zufolge hat, sind die Verhältnisse in diese Form der Verbindung sehr komplex. Zahlreichen theoretischen und experimentellen Untersuchungen in Deutschland und Frankreich bestätigen dies. Trotzdem ist das Verhalten von Vielschraubenverbindungen, wie das Verhalten der Einschraubenverbindungen, von den bisherigen Methoden nicht so gut, repräsentiert, um eine effektive Grundlage für den Konstrukteur zu schaffen. Ungünstig ist es, weil die Modelle wie das VDI-Modell eine lineare Variation der zusätzlichen Beanspruchungen (Zugkraft und Biegemoment) abhängig der äußeren Belastung ergeben und diese dann tipischerweise auch für niedrige Belastungen überschätzen, während bei der höheren Belastung übersehen, wie gefährlich sie sind.
De facto, im Falle einer auch mäßigen exzentrischen Belastung ist das lineare Modell von VDI 2230 nicht mehr anwendbar. Daraus folgt, dass VDI Model auf die Vielschraubenverbindungen nicht direkt übertragbar ist.
Aufgrund von diesem, stoßt die Auslegung einer hoch belasteten Schraubenverbindung sehr oft an die Grenzen, insbesondere wenn eine "Überdimensionieren" aus wirtschaftlichen, Gewichtsbegrenzungen und anderen Gründen keine brauchbare Option ist.
Die Grundlage der Prozedur
bezüglich der Bestimmung des sogenannten Krafteinleitungsfaktors ist strittig. Bei der zentrischen Vorspannung der
Verbindung wirken alle Kräfte, neben der Schraubenvorspannkraft FV und die Reaktionskraft in der Trennfuge FK,
entlang der Schraubenachse. Die verspannten Teile werden zusammengedruckt, wobei die maßgebende Nachgiebigkeit
![]() ist. Unter der exzentrischen äußeren Belastung trennt sich diese Wirkung (sieche Bild),
sodass für die Vorspannung (Montage) bestimmende Nachgiebigkeit aufgeteilt wird auf die Wirkung seitens der Schraubenkraft
und die Wirkung seitens der Kraft in der Trennfuge:
ist. Unter der exzentrischen äußeren Belastung trennt sich diese Wirkung (sieche Bild),
sodass für die Vorspannung (Montage) bestimmende Nachgiebigkeit aufgeteilt wird auf die Wirkung seitens der Schraubenkraft
und die Wirkung seitens der Kraft in der Trennfuge:
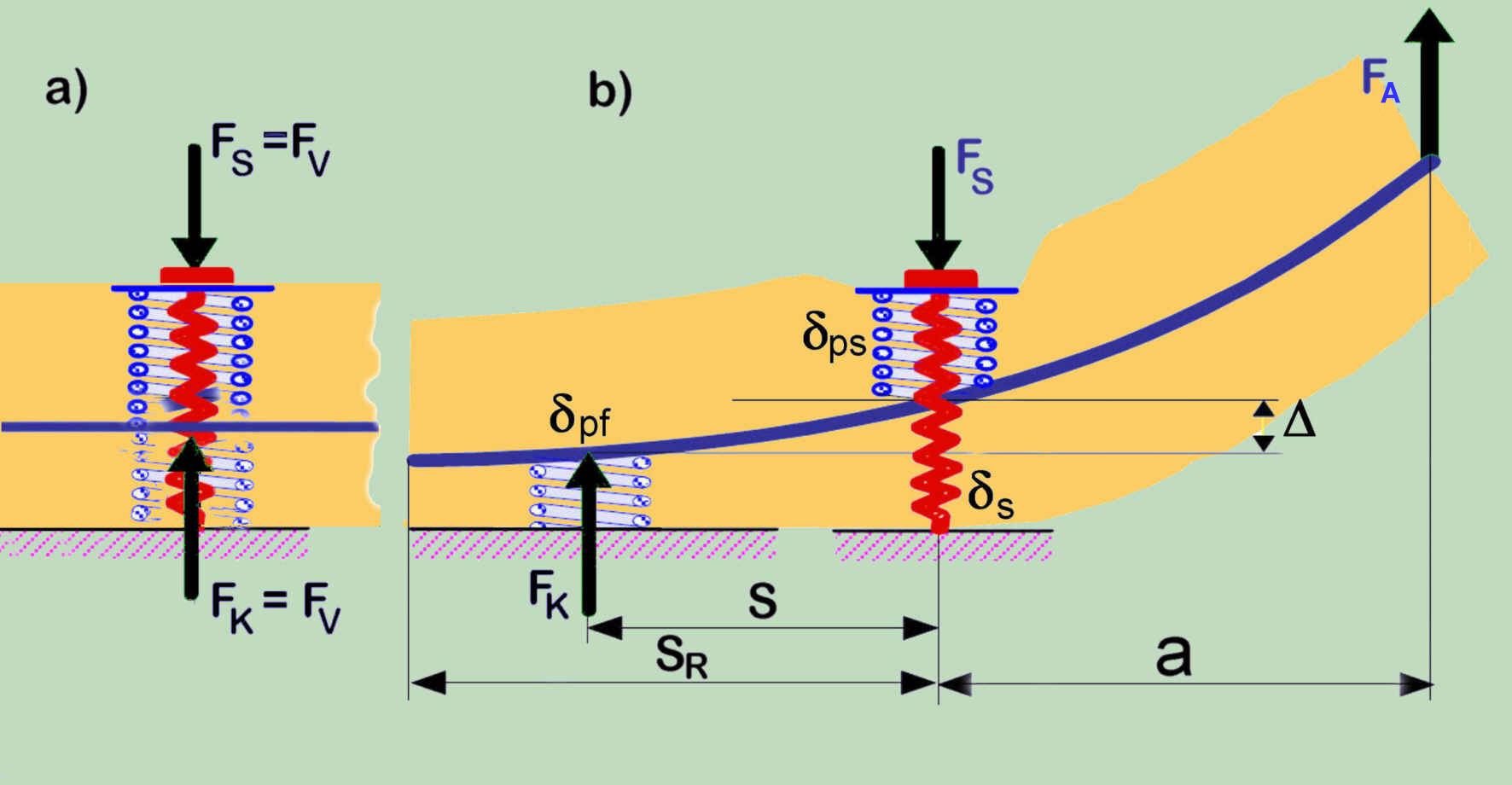
Klar, dass sich dieser Effekt anders manifestiert und deshalb nicht mit der Lage der Krafteinleitung der äußeren Kraft entlang, der Verbindungsachse zu tun hat. Ausgehend von der VDI Begründung musste der Konstrukteur im Falle der größeren Exzentrizität zu dem Schluss kommen, dass er den Effekt der Kraftanleitung vernachlässigen darf, obwohl eine sehr starke Wirkung, allerdings infolge der ganz anderen Zusammenhänge bleibt.
Diesbezügliche Zusammenhänge sind im Rahmen eines neuen Balkenmodells der Verbindungen analytisch erfasst:
Structural Integrity Analysis of Multi-Bolted Connection Using the Innovative Beam Model, in STRUCTURAL INTEGRITY AND LIFE, Vol. No. 3 (2011), pp. 147-156)und in den diesbezüglichen
Berechnungsbeispielen (freien Dawnloads für die beiden !)Die Eignung und die Notwendigkeit der Anwendung dieser Methode zur Analyse einer bestimmten Verbindung ist von der Steifigkeitsverhälnisen der Körper, die verbunden sind (Balken, Platte, etc.) anhängig.
Aus der Formel zur Bestimmung der Klemmkraft in der Verbindung (oben genannte Quellen)
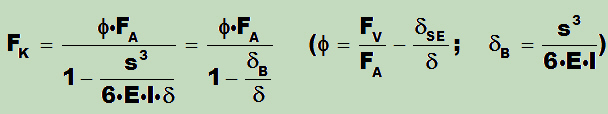
ist ersichtlich, dass nur wenn δB << δ, man die Einflüsse der Biegeverformung in der Verbindung vernachlässigen darf und die Anwendung klassischen linearen Modelle womöglich sinnvoll werden kann. Eine höhere Biegenachgiebigkeit bewirkt dagegen die signifikante Erhöhung der Klemmkraft in der Verbindung und eine wesentliche Erhöhung von allen Kräften in der Verbindung.
Weil die Veränderung der Klemmkraftexzentrizität (s) im Allgemeinen in einer Verbindung begrenzt ist (Randabstand) ist damit auch die maximale Erhöhung begrenzt. Allerdings ist die Steigerung der Kräfte danach noch schneller entsprechend dem Aufhebeln und Klaffen der Verbindung.
Weil die modernen Designs von der Leichtbau dominiert sind, bittet sich die Anwendung des vorgeschlagenen Balkenmodels für die meisten Fälle an.
Berücksichtigung von Biegeverformungen in der Verbindung, die durch typische außermittige Einführung der äußeren Belastung entstehen, stellt ein Wendepunkt in der Betrachtung von Schraubenverbindungen dar. Dadurch werden Rotscher’s Kegel, Lage der Krafteinleitung, etc. alleine keine maßgebenden Faktoren für das Verhalten einer Schraubeverbindung (außer für die Betrachtung der Vorspannung der Verbindung). Auch das Klaffen (Abheben) der Verbindung verändert sich gravierend.
Die Bestimmung der Exzentrizität "a" ist mit einem großen Risiko behaftet, weil die Schraubenverbindung nicht getrennt von der restlichen Struktur (Platte, Flansch, usw.) betrachtet werden kann. Wie bereits festgestellt an der Stelle der Einspannung der Verbindung an die restliche Struktur herrscht neben der Kraft auch ein Moment MB, das berücksichtigt werden muss und die Steifigkeitsverhältnisse in der Verbindung sind nicht von der restlichen Struktur unabhängig. Die Bestimmung in diese Hinsicht, die überhaupt nicht einfach ist, ist in den vielen Berechnungsmodellen dem Anwender überlassen, womit natürlich die potenziellen Fehlermöglichkeiten außergewöhnlich groß sind. Durch ungenauere Bestimmung dieses maßgebenden Parameters der Belastung werden die Ergebnisse der Berechnung infrage gestellt.
Es ist ein Trugschluss, man kann sich diesen allen Problemen auf eleganterweise entziehen, in dem man zur FE Methode greift. Im Gegenteil, bereits bei Modellierung zur FE Analyse nimmt man wahr, wie komplex eine Schraubenverbindung ist. Die Ergebnisse der Finite Elemente Analyse werden durch die Art der Modellierung der Verbindungsteile, Aufbringung der Vorspannung in der Verbindung, Berücksichtigung der Kontaktbedingungen in den Trennfugen, der Veränderungen der Lastverteilung und, nicht zu letzt, durch die Art der Berücksichtigung des nicht-linearen Verhaltens entscheidend beeinflusst.
Um Sie, bei der Gestaltung des FE-Models zu unterstützen, ohne dabei bei dem erforderlichen Aufwand die Genauigkeit der Ergebnisse infrage zu stellen, sind diesbezüglichen bedenklichen Punkte ausführlich hier behandelt.
Die analytische Bestimmung von Einflusskoeffizienten bi, das die Bedingungen an der Kopplung des Verbindungssegments an der Reststruktur wiedergibt, sollte hier beispielhaft an einer analytischen Lösung für die verschraubten Platte (oder Deckel) demonstriert werden.Für die Kreisplatte konstanten Dicke aufgrund von Roark’s Formulas for Stress and Strain (by W.C. Young and E.G. Budynas, Seventh Edition) aus der Tabelle 11.2, Case 13a (Seite 490) folgt (Unter der Verwendung von Symbolen θo = α and a = R)
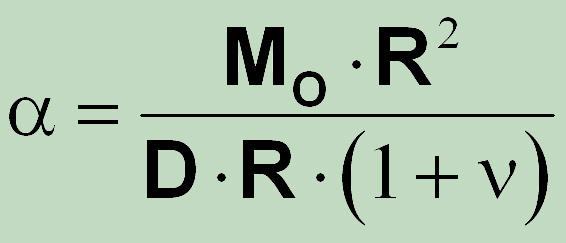
Nach der Berücksichtigung der Zahl der Schrauben, folgt für das Biegemomentanteil auf dem Schraubensegment
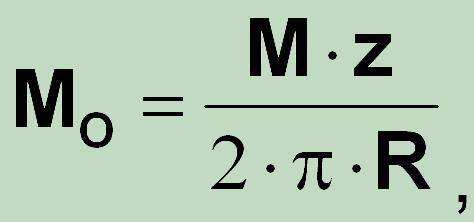
sodaß die obige Beziehung mehr allgemein geschrieben werden kann
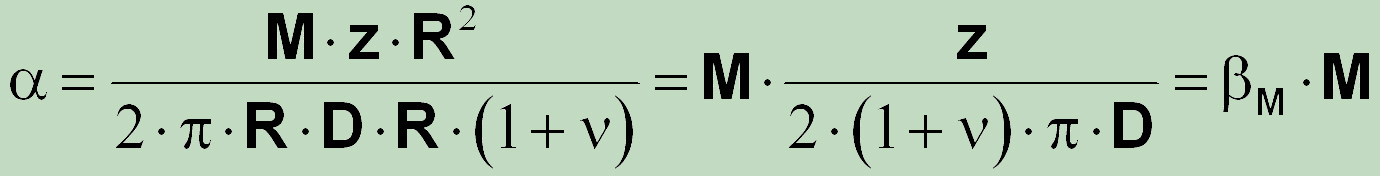
mit

Für die Bestimmung von
brauchen wir noch
![]()
Nach dem Einsetzen führt das zu dem Ergebnis
der zeigt, dass diese Einflusszahl an dem Anschlussdurchmesser basiert, der durch Verhältnis von Dicken der Basiskreisplatte und des Schraubensegments korrigiert wird.
Oder vereinfachend mit ![]()
Analytische Untersuchungen haben deutlich gezeigt, dass die Belastungsbedingungen in einer Verbindung nicht nur durch Verhältnis der Steifigkeiten in der Verbindung, sondern auch viel mehr durch das Verhältnis zwischen Vorspann- und Betriebskraft bestimmt werden. Demzufolge ist die Höhe der Vorspannung sehr wichtige Parameter für die Integrität der Strukturen mit Schraubenverbindungen.
Die hohe Empfindlichkeit von Schrauben gegenüber wechselnder Belastung, bedingt durch die aus dem Gewinde hervorgehende große Kerbwirkung, führt dazu, dass Schrauben, die eine zyklische Belastung ertragen müssen, hoch bis sehr hoch vorgespannt werden, um die Ermüdungsbeanspruchungen der Schrauben in der Verbindung zu eindämmen, was allerdings nur durch die nicht-lineare Berechnung berücksichtigt wird.
In der Praxis wird, durch das über-elastischen Vorspannen, dieser Tatsache die Rechnung schon seit Langem getragen. Nicht zuletzt geradezu bei den dynamisch beanspruchten Verbindungen in den Motorenbau, auch wenn dadurch das Niveau der Mittelspannung stark ansteigt. Offensichtlich ist in diesem Falle die Verminderung der Spannungsamplitude mehr ausschlaggebend.
Unabhängig davon soll berücksichtigt werden, dass im Betrieb, nach der Auflösung der äußeren Kräfte, die Schraubenvorspannung auf das ursprüngliche Niveau entlang der original Kurve (linearen elastischen Linie) zurückgeht, nur falls die maximale Schraubenspannung unterhalb der Streckgänze lag. Verhalten des Systems bleibt rein elastisch (unabhängig des nicht-linearen Verhaltens !!) nur, wenn die Gesamtbelastung im elastischen Bereich bleibt. Plastische Verformung der Schraube und der verspannten Teile durch eine Überlast wird immer zum Verlust der Vorspannung in der Verbindung führen. Das bedeutet, nach einer Belastung über die elastische Grenze werden alle späteren Lasten die höheren Lastanteile der Schraube in der Verbindung zufolge haben.
Darüber hinaus, bei den Werkstoffen, die sehr stark mittelspannungsabhängig reagieren, muss allerdings dieser Gesamtzusammenhang genauer untersucht werden.
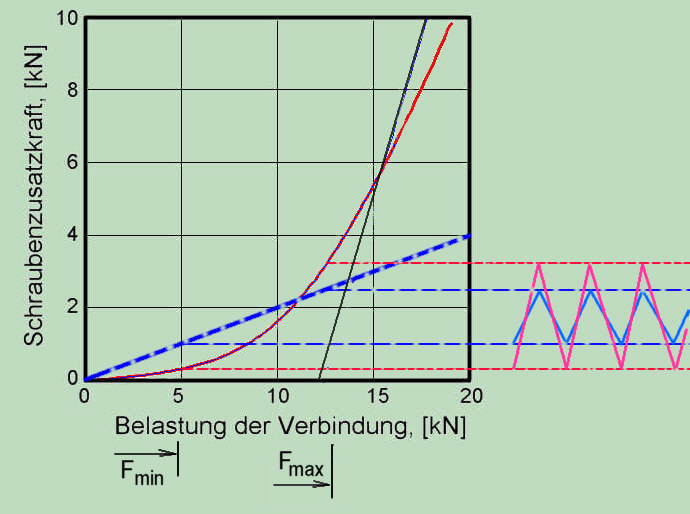
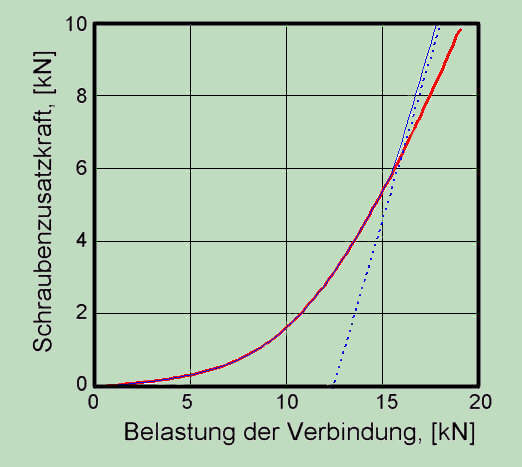
Berücksichtigung des nicht-linearen Verhaltens ist besonders wichtig für die dynamisch beanspruchten Verbindungen. Dieses kann am Beispiel vorangehender Berechnung demonstriert werden. Falls die äußere dynamische Betriebslast zwischen 5 und 12.5 kN variiert ergeben sich für die beiden Rechnungen - linear und nicht linear - erhebliche Unterschiede bezüglich der Spannungsamplitude. Die Erhöhung der Spannbreite kann sowohl in der Richtung des Spannungsminimums als auch in der Richtung von Spannungsmaximum entstehen, was in der Summe zu den beträchtlichen Unterschieden bezüglich der Amlitude der Ermüdungsbeanspruchung der Schraube führt. Deshalb lässt sich das auch nicht durch eine mehr konservative lineare Berechnung (größere Neigung der blauen Linie im Diagramm) vermeiden.
Bei den komplexen Strukturen ist es, des Weiteren üblich, die Werte, die zufälligen Einflüssen ausgesetzt sind (streuen), statistisch zu behandeln. Und das ist bezüglich der Hohe der Vorspannkraft wichtig. Insbesondere soll die Aufmerksamkeit der Tatsache getragen, dass die Vielschraubenverbindungen sehr oft durch Fail-Safe Verhalten dominiert werden, wo das Versagen einer Schraube durch die Tragfähigkeit benachbarten Schrauben (zumindest zeitbegrenzt) aufgefangen werden kann. Das heißt, für die Berücksichtigung der Streuung der Vorspannkraft ist es notwendig die Zahl der Schrauben und die Belastungsbedingungen in der Verbindung zu einbeziehen. Der Unterschied diesbezüglich, zum Beispiel, zwischen den statischen Rohrflansch und der Wellenflansch, die umlaufend beansprucht ist, ist offensichtlich.
Im Ergebnis, die sogenanten Anziehfaktoren für die Vielschraubenverbindung können nicht gleich, wie bei Einzelverbindung, sein.
Bekanntlich ein Teil des Setzen wird bei der Vorspannung durch steigende Anziehkraft ausgeglichen.Durch exzentrische äußere Belastung verlagert sich die Reaktionskraft mit zunehmender Belastung von der Verbindungsachse. Damit werden die neuen Kontaktflächen erschlossen, was auch zu den zusätzlichen Setzbeiträgen führt, die nicht mehr (während der Montage) ausgeglichen werden und demzufolge zu einer zusätzlichen Reduktion der Vorspannkraft in der Verbindung führt.
Bezüglich der Vielschraubenverbindungen ist das Hebelgesetz in seiner primitiven Form eine grobe Vereinfachung, die außerdem auf der unsicheren Seite ist und deshalb eigentlich nicht verwendet werden darf. Die Verfahrensweise die an dieser Annahme basieren („Kreisbogen“) sind genauso ungenau und auf der unsicheren Seite. Beziehungen, die für den mehr genauen Balkenmodel entwickelt wurden und die Versuche, zeigen, dass dieser Übergang immer die Form der Parabel annimmt.
Viel wichtiger ist es aber, dass dieses "Gesetz" auf Vielschraubenverbindungen sowieso nicht anwendbar wird, weil die Anschlüsse an die restliche Struktur nicht frei sind und das Drehen an diese Stelle nicht erfolgen kann ohne zusätzlicher Belastung der Verbindung.
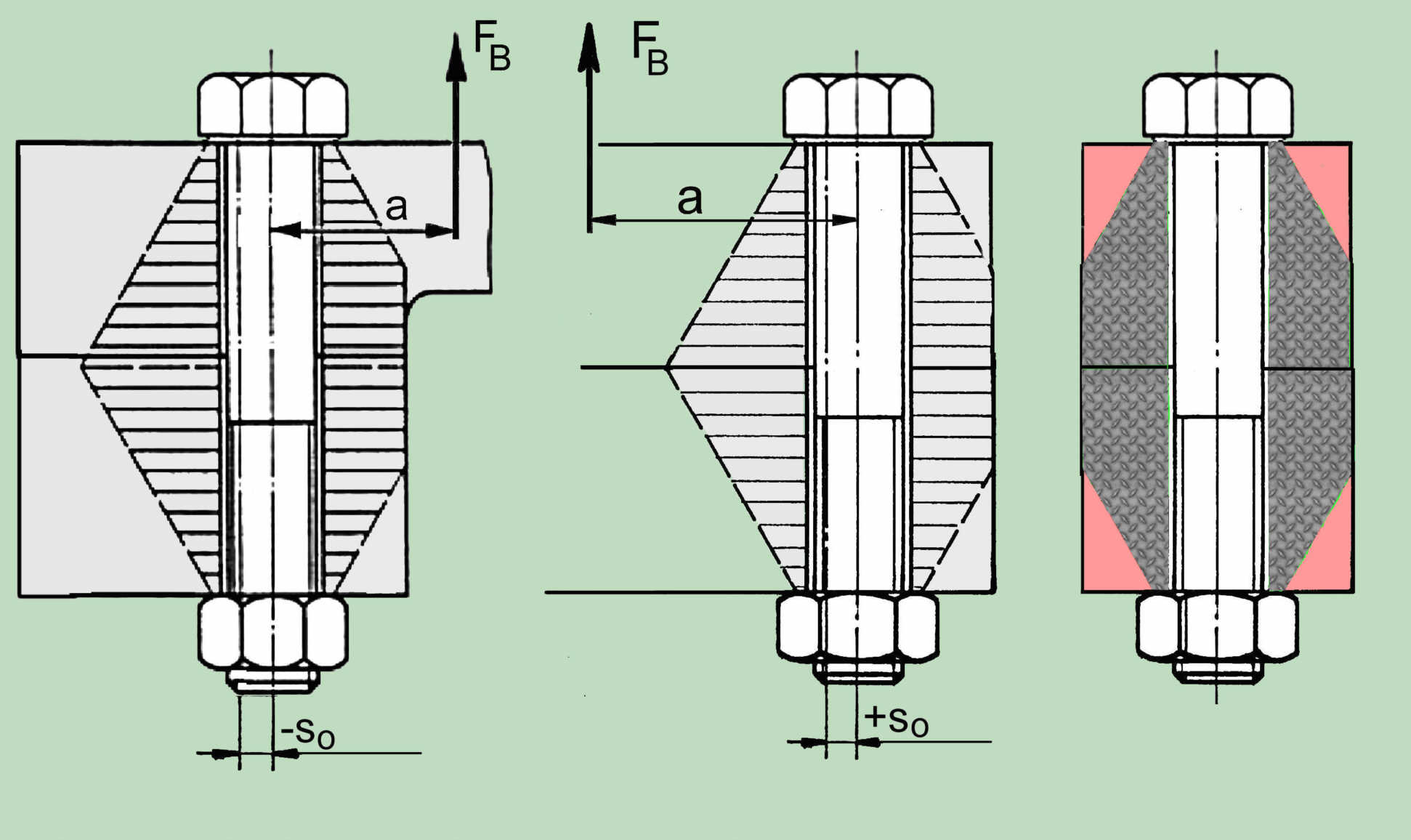
Einzelnen Verbindungen, bei welchen der sogenannten Verformungskegel an allen Seiten abgeschnitten ist, stellen der typische Fall der Verbindung mit den begrenzten Außenmaßen dar. Derartig schlanke zylindrische Verbindungen verhalten sich stark nicht-linear. Zur Behandlung derartigen Verbindungen ist die nicht-lineare Methode entwickelt worden [Konstruktion 27(1976) S. 192-97)], die leider aus der neuesten Auflage der VDI 2230 rausgenommen ist.
Nichtlineares Model zur Berechnung von zylindrischen EinscharaubenverbindungEs gibt kleine Zweifel, das die Schraubenverbindungen eine der maßgebenden Quellen der Nichtlinearität in mechanischen Strukturen sind. Dieses produziert erhebliche zusätzlichen Beanspruchung nicht nur für die Schrauben, sondern auch für die alle Teile in der Verbindung.
Obwohl lineare Modelle gewöhnlich konservative sind - dies ist bei den Verbindungen mit mehr als eine Schraube selten der Fall! Anwendung linearer Modelle auf kleine Belastungen führt zu über-konservativen Ergebnissen. Falls auch die höheren Belastungen zu erwarten sind, wird ihre Wirkung unterschätzt. In beiden Fällen die erreichbare Konstruktion misslingt.
Lineare Modelle sind falsch. Untersuchungen des Verhaltens bei der der Parametervariationen und -unsicherheiten mit einer falschen Modellform hat kein Sinn.
Vielleicht die wichtigste Unzulänglichkeit der bekannten Modelle ist, dass diesen die Funktion der Verbindung nur auf zwei Einflussparameter reduzieren: Nachgiebigkeit der Teile in Richtung der Schraubenachse und die Gewährleistung der ausrechenden minimallen Vorspannung. Alle anderen Einflussgroßen, wie die Biegesteifigkeit der angeschlossenen Teile (Platten, Zylinder etc.), wirkliche Lage (Exzentrizität) der äußeren Kraft, Höhe der Vorspannkraft und des Vorspannbiegemoments, das Einsetzen der erhöhten Beanspruchungen, weil die Verbindung nicht mehr intakt ist (Prying), blieben praktisch unberücksichtigt.
Darüber hinaus, sind die sicheren und aufwandgünstige Methoden, basieren an dem Balkenmodel für die Auslegung von Schraubenverbindung vorhanden. Von dem Autor, aufgrund der Berücksichtigung der grundlegenden Beziehungen der Festigkeitslehre, das erstvorgeschlagene Balkenmodell ist gegenüber seinen Ursprung, aufgrund der Erfahrungen aus der Praxis und der Untersuchungen von anderen Autoren, weiter entwickelt worden. Mithilfe dieses fortschriftlichen Models kann die Schraubenverbindung durch die Berücksichtigung des nicht-linearen Verhaltens und den Bedingungen für adäquate Funktion auf eine ausreichend genauere Art und Weise modelliert werden.
Sie wollen mehr darüber wissen ? Verständlich! Hollen Sie sich deshalb die ausführlich Unterlage zur